Every Measurement Comes with Some Amount of Uncertainty

Measurement uncertainty is characterized as the spread of values that can reasonably be attributed to the measurement.  This uncertainty can come from various sources – one of the most obvious being the uncertainty associated with rounding of a measurement.  Measurement instruments have a finite readability; thus, the measurement values that they display are necessarily rounded.  For example, let’s say that we have a balance with a capacity of 100 g and a readability of 0.1 g.  If we weigh an object and the display on the balance reads 10.0 g, one could think that it would be reasonable to say that this object weighs 10.0 g.  When in fact, the true weight measured could be anywhere between 9.95 g and 10.04 g.  That is a span of possible measurement values equaling 0.09 g, or almost 1% of the displayed measurement.  This is known as rounding error.  The uncertainty contributed by this rounding error is quantified by multiplying the readability of the balance by 0.41.  Rounding error is just one of many sources of uncertainty.  In order to know whether the uncertainty associated with a measurement is acceptable or not, accuracy requirements are set.  These requirements are known as tolerances, and are essentially the allowable amount of uncertainty for a given measurement.  As long as the uncertainty in a measurement does not exceed the tolerance limits, it is acceptable.

In regard to weighing, as we go lower on an instrument’s weighing range, the relative uncertainty associated with a measurement increases.  At the low end of a weighing instrument’s range, the dominant uncertainty influence is repeatability.  According to USP Chapter 1251, repeatability is the weighing instrument’s ability to display identical values for repeated weighings of the same object under the same conditions.  As a pharma industry requirement for balances used in qualitative/quantitative weighing, USP Chapter 41 states that repeatability be assessed by weighing a test weight at least 10 times; and that it is satisfied if the standard deviation of these measurements, multiplied by a coverage factor of 2, and divided by the desired smallest net weight is less than or equal to a tolerance of 0.10%.

repeatability = 2 x sd ÷ snw

If the standard deviation obtained is less than 0.41d, where d is the readability of the weighing instrument, then we substitute this value in for the standard deviation in the above formula.  This 0.41d value – representing the uncertainty from rounding error – acts as a floor for the standard deviation.

If we use a low enough net sample weight, the uncertainty associated with the repeatability measurement becomes higher than the allowable uncertainty – or tolerance.  This brings up an important concept: Minimum Weight.  The minimum weight is the least amount of material that can be weighed on an instrument resulting in uncertainty that is not greater than the required tolerance.

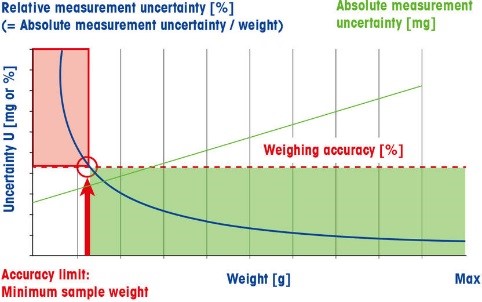
According to USP Chapter 1251, we can find this value by multiplying the standard deviation by the coverage factor and dividing by the required tolerance.  Once again, we would use the 0.41d value if it is larger than the standard deviation.  When adhering to USP Chapter 41, where the coverage factor is specified to be 2 and the required tolerance is 0.10%, the minimum weight formula simplifies to:

Min Wt = 2000 * sd

To satisfy the tolerance requirements, the smallest net weight to be used on a particular weighing instrument must be greater than or equal to the minimum weight.  Because the standard deviation found in repeatability testing can be influenced by many factors, such as the operator and the environment, the minimum weight is not a stable value.  Thus, it is always recommended to weigh above the minimum weight.